每天一道在线编程题
问题:Median of Two Sorted Arrays
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
Example 1:
nums1 = [1, 3] nums2 = [2]
The median is 2.0
Example 2:
nums1 = [1, 2] nums2 = [3, 4]
The median is (2 + 3)/2 = 2.5
总体分析:
本问题要求的时间复杂度决定了不可能使用任何排序方法(因为排序方法的时间复杂度下限已经超过了要求),再仔细看下时间复杂度要求, 不难想到二分法。
解决方案一:(C语言)
分析: 本问题是寻找已经提增排序的两数列的中位数,当所有数的个数为奇数是就是中间的那个数,当为偶数时则为中间两个数的平均值。 方案一就是利用这个思想把问题转化为寻找两个有序数组求第N大数的过程。具体而言,对于奇数则只需寻找第(总数/2+1)大数即可,而对于 偶数则还需要寻找第(总数/2)大数,这两个数求均值即可。
函数:kthsmallest
/*********************************************
**本函数功能:求第k小的数
** 输入:两个递增数列及其他们的长度
** 输出:返回这两个数组的第k大数
*********************************************/
int kthsmallest(int *a,int m,int *b,int n,int k) {
if (m == 0) {
return b[k - 1];
}
if (n == 0) {
return a[k - 1];
}
if (k == 1) {
return (a[0] < b[0])?a[0]:b[0];
}
if (k == m + n) {
return (a[m - 1] > b[n - 1])?a[m - 1]:b[n - 1];
}
int i = ((double) m) / (m + n) * (k - 1);
int j = k - 1 - i;
if (j >= n) {
j = n - 1;
i = k - n;
}
if (((i == 0) || (a[i - 1] <= b[j])) && (b[j] <= a[i])) {
return b[j];
}
if (((j == 0) || (b[j - 1] <= a[i])) && (a[i] <= b[j])) {
return a[i];
}
if (a[i] <= b[j]) {
return kthsmallest(a + i + 1, m - i - 1, b, j, k - i - 1);
} else {
return kthsmallest(a, i, b + j + 1, n - j - 1, k - j - 1);
}
}函数:findMedianSortedArrays
/*********************************************
**本函数功能:求两个递增数组的中位数
** 输入:两个递增数列及其他们的长度
** 输出:返回这两个数组的中位数
*********************************************/
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
int medianOrder=(nums1Size+nums2Size)/2+1;
double median=0.0;
int max1=0,max2=0;
max1=kthsmallest(nums1,nums1Size,nums2,nums2Size,medianOrder);
max2=max1; //默认奇数(原因见分析:奇偶有相同操作,偶多了一步),此时为了统一下面的第三行/2的形式
if((nums1Size+nums2Size)%2==0) //偶数特有的操作
max2=kthsmallest(nums1,nums1Size,nums2,nums2Size,medianOrder-1);
median=(double)(max1+max2)/2;
return median;
}运行效率:
函数kthsmallest中用到了递归,这样虽然容易理解,但会影响时间空间效率。不过在递归深度不大的时候影响不明显, 在与之后的方案比较证明了这一点(测试数据比较少,用的数组长度也比较短,从而减少了递归深度)。
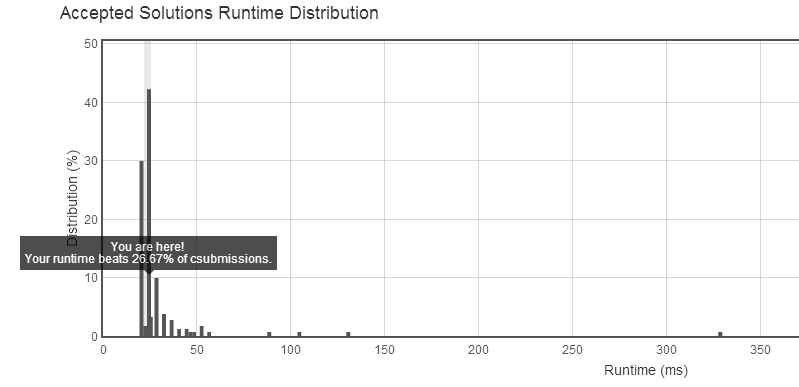
解决方案二:
分析:本方案发现,不论是奇数个还是偶数个,反正都要用到中间的一个或两个数,干脆把这两个数都存起来,然后再来 判断奇偶,还发现,两个数组中间的那个数的大小比较以及较大的那个数在较小的那个数所在数组的位序决定了我们要求的 中位数的位置。具体说来,(假设这两个数组为A、B)假设A的中间数a(偶数时取较小的中间数)大于B的中间数b,则a的位序 ath,a在B中的二分插入的位序为a_in_B,两个数组合起来的中间数位序为medianOrder(即:总个数/2),则有以下规律:令 i=ath-medianOrder+a_in_B,有,所求即为ath之前和a_in_B之前的两个数组的第i大数(不过要分情况,这里的i=0,i<0,i>0 还有A,B中数的个数为奇数偶数时中间数的位序计算式子不同)。详细请看下面的程序。
函数:binary_search
/*********************************************
** 函数:binary_search
** 功能:求一个数二分插入一递增数组的位序
** 输入:数组及其起止下标,待插入的数
** 输出:返回待插入数在数组中的位序
*********************************************/
int binary_search(int* array, int start,int end, int goal)
{
int low = start;
int high = end;
int middle=0;
while (low <= high)
{
middle = (high - low) / 2 + low; // 直接使用(high + low) / 2 可能导致溢出
if (array[middle] == goal)
return middle+1;
//在左半边
else if (array[middle] > goal)
high = middle - 1;
//在右半边
else
low = middle + 1;
}
//没找到返回插入位置
return low;
}函数:findKthBiggest
/*********************************************
** 函数: findKthBiggest
** 功能:求两个递增数组倒数第Kth及Kth-1大数
** 输入:两数组首地址及其长度,Kth及存放Kth和Kth-1大数的数组result
** 输出:返回1,表示输入有误,返回0,正常结束
*********************************************/
int findKthBiggest(int *arrA,int sizeA,int *arrB,int sizeB,int Kth,int *result)
{
long int size=sizeA+sizeB;
int Nth=Kth;
int na=sizeA-1,nb=sizeB-1;
result[0]=1;
if(Kth<=0 || sizeA<0 || sizeB<0 || Kth>size)
{
result[0]=0;
return 1;
}
if(sizeA==0 || sizeB==0)
{
int *arr=arrA;
int arrSize=sizeA;
if(sizeA==0)
{
arr=arrB;
arrSize=sizeB;
}
Nth=arrSize-Kth;
result[1]=arr[Nth];
if(Nth)
{
result[2]=arr[Nth-1];
result[0]=2;
}
return 0;
}
while(Nth)
{
if(na<0 || nb<0)
{
int *arr=arrA;
int arrSize=na;
if(na<0)
{
arr=arrB;
arrSize=nb;
}
Nth=arrSize-Nth+1;
result[1]=arr[Nth];
result[0]=1;
if(Nth)
{
result[2]=arr[Nth-1];
result[0]=2;
}
break;
}
else
{
if(arrA[na]>arrB[nb])
{
result[1]=arrA[na];
na--;
}
else
{
result[1]=arrB[nb];
nb--;
}
}
Nth--;
}
if(result[0]<2)
{
if(na<0 || nb<0)
{
int *arr=arrA;
int arrSize=na;
if(na<0)
{
arr=arrB;
arrSize=nb;
}
result[2]=arr[arrSize];
}
else
{
if(arrA[na]>arrB[nb])
result[2]=arrA[na];
else
result[2]=arrB[nb];
}
}
return 0;
}函数:findMedianSortedArrays
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
double median=0.0;
//数组中数为偶数时中间数的位序计算
int mid1=nums1Size/2-1, mid2=nums2Size/2-1;
long int size=nums1Size+nums2Size;
int medianOrder=size/2;
int mid1_in_nums2=0,mid2_in_nums1=0;
int i=0;
int result[]={0,0,0};
//数组中数为奇数时中间数的位序计算
if(nums1Size%2)
mid1=(nums1Size-1)/2;
if(nums2Size%2)
mid2=(nums2Size-1)/2;
//其中一个数组为空时
if( nums1Size == 0 || nums2Size == 0)
{
int mid=0;
if(size % 2)
{
mid = size / 2;
median = (nums1Size == 0) ? \
nums2[mid] : nums1[mid];
}
else
{
mid1 =size /2 ;
mid2 = mid1 - 1;
median = (nums1Size == 0) ? \
(double)(nums2[mid1] + nums2[mid2])/2 :(double)(nums1[mid1] + nums1[mid2])/2;
}
return median;
}
//比较两个数组中间数的大小
if(nums1[mid1]>nums2[mid2])
{
//求大的中间数在另一个数组中的二分插入的位序
mid1_in_nums2=binary_search(nums2, mid2+1,nums2Size-1, nums1[mid1]);
i=mid1_in_nums2-medianOrder+mid1;
//根据i的不同情况进行处理
if(i>0)
findKthBiggest(nums1,mid1,nums2,mid1_in_nums2,i,result);
else if(i<0)
{
findKthBiggest(nums1,mid1-i+1,nums2,mid1_in_nums2-i,-i+1,result);
}
else
findKthBiggest(nums1,mid1+1,nums2,mid1_in_nums2,i+1,result);
}
else
{
mid2_in_nums1=binary_search(nums1, mid1+1,nums1Size-1, nums2[mid2]);
i=mid2_in_nums1-medianOrder+mid2;
if(i>0)
{
findKthBiggest(nums2,mid2,nums1,mid2_in_nums1,i,result);
}
else if(i<0)
{
findKthBiggest(nums2,mid2-i+1,nums1,mid2_in_nums1-i,-i+1,result);
}
else
findKthBiggest(nums2,mid2+1,nums1,mid2_in_nums1,i+1,result);
}
//对两个数组个数的总数为奇数偶数时做不同处理
if(size%2)
median=result[1];
else
median=(double)(result[1]+result[2])/2;
return median;
}方案评价:
本方案较方案一效率有所提升(在递归深度较小时不明显),但逻辑相对来说复杂很多,稍微走神一下可能会导致编写的程序逻辑混乱而 达不到想要的结果,说实话,博主也是跟踪调试了很久才成的,而且用了多组测试数据。而且要求基本功很扎实。
【注意】本文属于作者原创,欢迎转载!转载时请注明以下内容:
(转载自)ShengChangJian's Blog编程技术文章地址:
https://ShengChangJian.github.io/2016/07/Median-of-Two-Sorted-Arrays.html
主页地址:https://shengchangjian.github.io/